Serendip

Web Studio

問題2.42

どうしてもわからなかったので、 SICP memo: 問題2.42 – 素人くさいSICP「独」書会 の解答を見て、Exercise 2.42 エイトクイーンパズル完全攻略 – Yet Another わっほい を参考にして手続きの働き方を調べてみた。

(define (queens board-size)
  (define (queen-cols k)
    (if (= k 0)
        (list empty-board)
        (filter
          (lambda (positions) (print "positions: " positions) (safe? k positions))
          (flatmap
            (lambda (rest-of-queens)
                    (print "rest-of-queens: " rest-of-queens) (map (lambda (new-row)
                                 (adjoin-position new-row k rest-of-queens))
                         (enumerate-interval 1 board-size)))
            (queen-cols (- k 1))))))
  (queen-cols board-size))

(define empty-board ())

(define (adjoin-position row col rest)
  (cons (list row col) rest))

(define (safe? k positions)
  (let ((kth (car positions)))
       (define (iter rest)
         (print "kth " kth ", rest: " rest)
         (cond ((null? rest) #t)
               ((conflicts? (car rest) kth) #f)
               (else (iter (cdr rest)))))
       (iter (cdr positions))))

(define (conflicts? a b)
  (let ((dx (abs (- (car a) (car b))))
        (dy (abs (- (cadr a) (cadr b)))))
       (cond ((= dx 0) #t)
             ((= dy 0) #t)
             ((= dx dy) #t)
             (else #f))))

まず、再帰で k=0 になるまで降りていく。
k=0 で () が返ってくる。

続いて k=1 の再帰部分では、手続き adjoin-position で (cons (list new-row k) rest-of-queens) の処理を行う。
new-row は (1 2 3 4) 、 k は 1
(cons (list '(1 2 3 4) 1) ())
(((1 2 3 4) 1))

位置の集合 () に新しい場所の座標 (1 2 3 4) を連結する。
(map (lambda (new-row) (cons (list new-row 1) ())) '(1 2 3 4))
(((1 1)) ((2 1)) ((3 1)) ((4 1)))

フィルタでクイーンを置くことのできる場所を求める。
(filter (lambda (positions) (safe? 1 positions)) '(((1 1)) ((2 1)) ((3 1)) ((4 1))))
(((1 1)) ((2 1)) ((3 1)) ((4 1)))
最初の列では全ての場所にクイーンを置くことが可能となる。

次に k=2 の再帰部分に移る。rest-of-queens の内のひとつ ((1 1)) の場合を見てみる。
new-row は (1 2 3 4) 、 k は 2
(cons (list '(1 2 3 4) 2) '((1 1)))
(((1 2 3 4) 2) (1 1))

位置の集合 ((1 1)) に新しい場所の座標 (1 2 3 4) を連結する。
(map (lambda (new-row) (cons (list new-row 2) '(((1 1))))) '(1 2 3 4))
(((1 2) ((1 1))) ((2 2) ((1 1))) ((3 2) ((1 1))) ((4 2) ((1 1))))

flatmap でリストの入れ子状態を解消する。
(flatmap (lambda (rest-of-queens) (map (lambda (new-row) (adjoin-position new-row 2 rest-of-queens)) '(1 2 3 4))) '(((1 1))))
(((1 2) (1 1)) ((2 2) (1 1)) ((3 2) (1 1)) ((4 2) (1 1)))

フィルタでクイーンを置くことのできる場所を求める。
(filter (lambda (positions) (safe? 1 positions)) '(((1 2) (1 1)) ((2 2) (1 1)) ((3 2) (1 1)) ((4 2) (1 1))))
(((3 2) (1 1)) ((4 2) (1 1)))

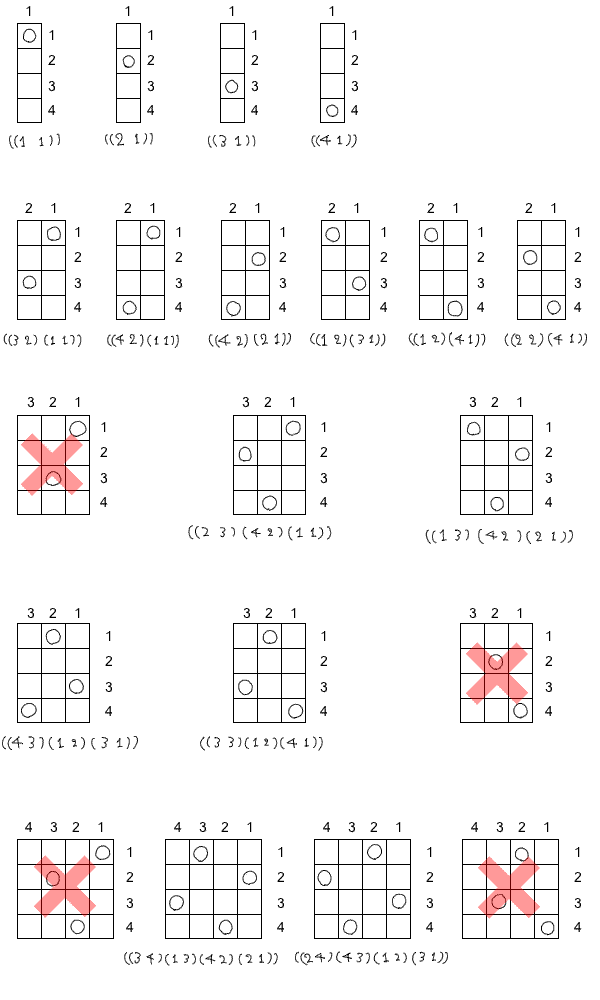
同様にして (2 1)、(3 1)、 (4 1) の場合についても評価して行き、次の再帰に移って行き、最終的に残ったリストがパズルの解答となる。

(queens 4)

gosh> rest-of-queens: ()
positions: ((1 1))
kth (1 1), rest: ()
positions: ((2 1))
kth (2 1), rest: ()
positions: ((3 1))
kth (3 1), rest: ()
positions: ((4 1))
kth (4 1), rest: ()
rest-of-queens: ((1 1))
rest-of-queens: ((2 1))
rest-of-queens: ((3 1))
rest-of-queens: ((4 1))
positions: ((1 2) (1 1))
kth (1 2), rest: ((1 1))
positions: ((2 2) (1 1))
kth (2 2), rest: ((1 1))
positions: ((3 2) (1 1))
kth (3 2), rest: ((1 1))
kth (3 2), rest: ()
positions: ((4 2) (1 1))
kth (4 2), rest: ((1 1))
kth (4 2), rest: ()
positions: ((1 2) (2 1))
kth (1 2), rest: ((2 1))
positions: ((2 2) (2 1))
kth (2 2), rest: ((2 1))
positions: ((3 2) (2 1))
kth (3 2), rest: ((2 1))
positions: ((4 2) (2 1))
kth (4 2), rest: ((2 1))
kth (4 2), rest: ()
positions: ((1 2) (3 1))
kth (1 2), rest: ((3 1))
kth (1 2), rest: ()
positions: ((2 2) (3 1))
kth (2 2), rest: ((3 1))
positions: ((3 2) (3 1))
kth (3 2), rest: ((3 1))
positions: ((4 2) (3 1))
kth (4 2), rest: ((3 1))
positions: ((1 2) (4 1))
kth (1 2), rest: ((4 1))
kth (1 2), rest: ()
positions: ((2 2) (4 1))
kth (2 2), rest: ((4 1))
kth (2 2), rest: ()
positions: ((3 2) (4 1))
kth (3 2), rest: ((4 1))
positions: ((4 2) (4 1))
kth (4 2), rest: ((4 1))
rest-of-queens: ((3 2) (1 1))
rest-of-queens: ((4 2) (1 1))
rest-of-queens: ((4 2) (2 1))
rest-of-queens: ((1 2) (3 1))
rest-of-queens: ((1 2) (4 1))
rest-of-queens: ((2 2) (4 1))
positions: ((1 3) (3 2) (1 1))
kth (1 3), rest: ((3 2) (1 1))
kth (1 3), rest: ((1 1))
positions: ((2 3) (3 2) (1 1))
kth (2 3), rest: ((3 2) (1 1))
positions: ((3 3) (3 2) (1 1))
kth (3 3), rest: ((3 2) (1 1))
positions: ((4 3) (3 2) (1 1))
kth (4 3), rest: ((3 2) (1 1))
positions: ((1 3) (4 2) (1 1))
kth (1 3), rest: ((4 2) (1 1))
kth (1 3), rest: ((1 1))
positions: ((2 3) (4 2) (1 1))
kth (2 3), rest: ((4 2) (1 1))
kth (2 3), rest: ((1 1))
kth (2 3), rest: ()
positions: ((3 3) (4 2) (1 1))
kth (3 3), rest: ((4 2) (1 1))
positions: ((4 3) (4 2) (1 1))
kth (4 3), rest: ((4 2) (1 1))
positions: ((1 3) (4 2) (2 1))
kth (1 3), rest: ((4 2) (2 1))
kth (1 3), rest: ((2 1))
kth (1 3), rest: ()
positions: ((2 3) (4 2) (2 1))
kth (2 3), rest: ((4 2) (2 1))
kth (2 3), rest: ((2 1))
positions: ((3 3) (4 2) (2 1))
kth (3 3), rest: ((4 2) (2 1))
positions: ((4 3) (4 2) (2 1))
kth (4 3), rest: ((4 2) (2 1))
positions: ((1 3) (1 2) (3 1))
kth (1 3), rest: ((1 2) (3 1))
positions: ((2 3) (1 2) (3 1))
kth (2 3), rest: ((1 2) (3 1))
positions: ((3 3) (1 2) (3 1))
kth (3 3), rest: ((1 2) (3 1))
kth (3 3), rest: ((3 1))
positions: ((4 3) (1 2) (3 1))
kth (4 3), rest: ((1 2) (3 1))
kth (4 3), rest: ((3 1))
kth (4 3), rest: ()
positions: ((1 3) (1 2) (4 1))
kth (1 3), rest: ((1 2) (4 1))
positions: ((2 3) (1 2) (4 1))
kth (2 3), rest: ((1 2) (4 1))
positions: ((3 3) (1 2) (4 1))
kth (3 3), rest: ((1 2) (4 1))
kth (3 3), rest: ((4 1))
kth (3 3), rest: ()
positions: ((4 3) (1 2) (4 1))
kth (4 3), rest: ((1 2) (4 1))
kth (4 3), rest: ((4 1))
positions: ((1 3) (2 2) (4 1))
kth (1 3), rest: ((2 2) (4 1))
positions: ((2 3) (2 2) (4 1))
kth (2 3), rest: ((2 2) (4 1))
positions: ((3 3) (2 2) (4 1))
kth (3 3), rest: ((2 2) (4 1))
positions: ((4 3) (2 2) (4 1))
kth (4 3), rest: ((2 2) (4 1))
kth (4 3), rest: ((4 1))
rest-of-queens: ((2 3) (4 2) (1 1))
rest-of-queens: ((1 3) (4 2) (2 1))
rest-of-queens: ((4 3) (1 2) (3 1))
rest-of-queens: ((3 3) (1 2) (4 1))
positions: ((1 4) (2 3) (4 2) (1 1))
kth (1 4), rest: ((2 3) (4 2) (1 1))
positions: ((2 4) (2 3) (4 2) (1 1))
kth (2 4), rest: ((2 3) (4 2) (1 1))
positions: ((3 4) (2 3) (4 2) (1 1))
kth (3 4), rest: ((2 3) (4 2) (1 1))
positions: ((4 4) (2 3) (4 2) (1 1))
kth (4 4), rest: ((2 3) (4 2) (1 1))
kth (4 4), rest: ((4 2) (1 1))
positions: ((1 4) (1 3) (4 2) (2 1))
kth (1 4), rest: ((1 3) (4 2) (2 1))
positions: ((2 4) (1 3) (4 2) (2 1))
kth (2 4), rest: ((1 3) (4 2) (2 1))
positions: ((3 4) (1 3) (4 2) (2 1))
kth (3 4), rest: ((1 3) (4 2) (2 1))
kth (3 4), rest: ((4 2) (2 1))
kth (3 4), rest: ((2 1))
kth (3 4), rest: ()
positions: ((4 4) (1 3) (4 2) (2 1))
kth (4 4), rest: ((1 3) (4 2) (2 1))
kth (4 4), rest: ((4 2) (2 1))
positions: ((1 4) (4 3) (1 2) (3 1))
kth (1 4), rest: ((4 3) (1 2) (3 1))
kth (1 4), rest: ((1 2) (3 1))
positions: ((2 4) (4 3) (1 2) (3 1))
kth (2 4), rest: ((4 3) (1 2) (3 1))
kth (2 4), rest: ((1 2) (3 1))
kth (2 4), rest: ((3 1))
kth (2 4), rest: ()
positions: ((3 4) (4 3) (1 2) (3 1))
kth (3 4), rest: ((4 3) (1 2) (3 1))
positions: ((4 4) (4 3) (1 2) (3 1))
kth (4 4), rest: ((4 3) (1 2) (3 1))
positions: ((1 4) (3 3) (1 2) (4 1))
kth (1 4), rest: ((3 3) (1 2) (4 1))
kth (1 4), rest: ((1 2) (4 1))
positions: ((2 4) (3 3) (1 2) (4 1))
kth (2 4), rest: ((3 3) (1 2) (4 1))
positions: ((3 4) (3 3) (1 2) (4 1))
kth (3 4), rest: ((3 3) (1 2) (4 1))
positions: ((4 4) (3 3) (1 2) (4 1))
kth (4 4), rest: ((3 3) (1 2) (4 1))
(((3 4) (1 3) (4 2) (2 1)) ((2 4) (4 3) (1 2) (3 1)))
gosh>

計算機プログラムの構造と解釈

posted with amazlet at 08.11.07

ジェラルド・ジェイ サスマン ジュリー サスマン ハロルド エイブルソン
ピアソンエデュケーション
売り上げランキング: 6542

Amazon.co.jp で詳細を見る