Serendip

Web Studio

問題2.10

最初に思いついた解答

(define (div-interval x y)
  (if (and (< (lower-bound y) 0) (> (upper-bound y) 0))
      (error "error")
      (mul-interval x
                    (make-interval (/ 1.0 (upper-bound y))
                                   (/ 1.0 (lower-bound y))))))

零を跨る区間の判定を簡単にした。

(define (div-interval x y)
  (if (< (* (lower-bound y) (upper-bound y)) 0)
      (error "error")
      (mul-interval x
                    (make-interval (/ 1.0 (upper-bound y))
                                   (/ 1.0 (lower-bound y))))))

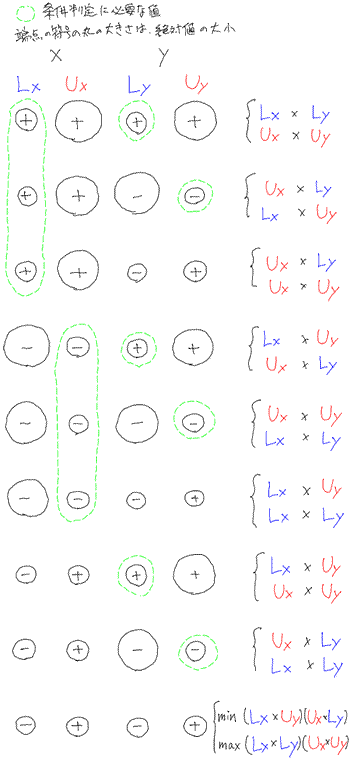
問題2.11

(define (mul-interval x y)
  (let ((lbx (lower-bound x))
        (ubx (upper-bound x))
        (lby (lower-bound y))
        (uby (upper-bound y)))
       (cond ((> lbx 0) ; x が正
              (cond ((> lby 0) ; y が正
                     (make-interval (* lbx lby)
                                    (* ubx uby)))
                    ((< uby 0) ; y が負
                     (make-interval (* ubx lby)
                                    (* lbx uby)))
                    (else ; y が零を跨る
                      (make-interval (* ubx lby)
                                     (* ubx uby)))))
             ((< ubx 0) ; x が負
              (cond ((> lby 0) ; y が正
                     (make-interval (* lbx uby)
                                    (* ubx lby)))
                    ((< uby 0) ; y が負
                     (make-interval (* ubx uby)
                                    (* lbx lby)))
                    (else ; y が零を跨る
                      (make-interval (* lbx uby)
                                     (* lbx lby)))))
             (else ; x が零を跨る
               (cond ((> lby 0) ; y が正
                      (make-interval (* lbx uby)
                                     (* ubx uby)))
                     ((< uby 0) ; y が負
                      (make-interval (* ubx lby)
                                     (* lbx lby)))
                     (else ; y が零を跨る
                       (make-interval (min (* lbx uby) (* ubx lby))
                                      (max (* lbx lby) (* ubx uby)))))))))

計算機プログラムの構造と解釈

posted with amazlet at 08.11.07

ジェラルド・ジェイ サスマン ジュリー サスマン ハロルド エイブルソン
ピアソンエデュケーション
売り上げランキング: 6542

Amazon.co.jp で詳細を見る