Serendip

Web Studio

問題1.35

(define tolerance 0.00001)

(define (fixed-point f first-guess)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) tolerance))
  (define (try guess)
    (let ((next (f guess)))
         (if (close-enough? guess next)
             next
             (try next))))
  (try first-guess))

(fixed-point (lambda (x) (+ 1 (/ 1 x))) 1.0)

gosh> 1.6180327868852458

問題1.36

平均緩和法を使わなかった場合は35ステップ、使った場合は10ステップとなる。

(define tolerance 0.00001)

(define (fixed-point f first-guess)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) tolerance))
  (define (try guess)
    (let ((next (f guess)))
         (display next)
         (newline)
         (if (close-enough? guess next)
             next
             (try next))))
  (try first-guess))

(fixed-point (lambda (x) (/ (log 1000) (log x))) 2.0)

(define (average x y) (/ (+ x y) 2))

gosh> 9.965784284662087
3.004472209841214
6.279195757507157
3.759850702401539
5.215843784925895
4.182207192401397
4.8277650983445906
4.387593384662677
4.671250085763899
4.481403616895052
4.6053657460929
4.5230849678718865
4.577114682047341
4.541382480151454
4.564903245230833
4.549372679303342
4.559606491913287
4.552853875788271
4.557305529748263
4.554369064436181
4.556305311532999
4.555028263573554
4.555870396702851
4.555315001192079
4.5556812635433275
4.555439715736846
4.555599009998291
4.555493957531389
4.555563237292884
4.555517548417651
4.555547679306398
4.555527808516254
4.555540912917957
4.555532270803653
4.555532270803653

平均緩和法を使った場合

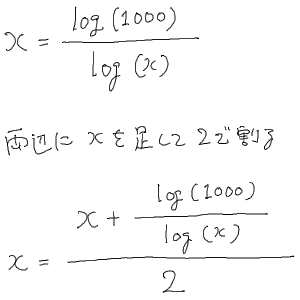
(fixed-point (lambda (x) (average x (/ (log 1000) (log x)))) 2.0)

gosh> 5.9828921423310435
4.922168721308343
4.628224318195455
4.568346513136242
4.5577305909237005
4.555909809045131
4.555599411610624
4.5555465521473675
4.555537551999825
4.555537551999825

問題1.37

4桁の精度の近似を得るためには k が11以上であればよい。

(define (cont-frac n d k)
  (define (iter i)
    (if (= i k)
        (/ (n i) (d i))
        (/ (n i) (+ (d i) (iter (+ i 1))))))
  (iter 1))

(define (iter-a-to-b f a b)
  (newline)
  (display a)
  (display " -> ")
  (if (> a b)
      (f a)
      (and (display (f a)) (iter-a-to-b f (+ a 1) b))))

(iter-a-to-b
  (lambda (k)
          (cont-frac (lambda (i) 1.0)
                     (lambda (i) 1.0)
                     k))
  1
  20)

gosh> 
1 -> 1.0
2 -> 0.5
3 -> 0.6666666666666666
4 -> 0.6000000000000001
5 -> 0.625
6 -> 0.6153846153846154
7 -> 0.6190476190476191
8 -> 0.6176470588235294
9 -> 0.6181818181818182
10 -> 0.6179775280898876
11 -> 0.6180555555555556
12 -> 0.6180257510729613
13 -> 0.6180371352785146
14 -> 0.6180327868852459
15 -> 0.6180344478216819
16 -> 0.6180338134001252
17 -> 0.6180340557275542
18 -> 0.6180339631667064
19 -> 0.6180339985218034
20 -> 0.6180339850173578
21 -> 0.6180339901755971

反復的プロセスの場合。

(define (cont-frac-re n d k)
  (define (cont-frac-iter i result)
    (if (= i k)
        result
        (cont-frac-iter (+ i 1) (/ (n i) (+ (d i) result)))))
  (cont-frac-iter 1 0))

(iter-a-to-b
  (lambda (k)
          (cont-frac-re (lambda (i) 1.0)
                        (lambda (i) 1.0)
                        k))
  1
  20)

gosh> 
1 -> 0
2 -> 1.0
3 -> 0.5
4 -> 0.6666666666666666
5 -> 0.6000000000000001
6 -> 0.625
7 -> 0.6153846153846154
8 -> 0.6190476190476191
9 -> 0.6176470588235294
10 -> 0.6181818181818182
11 -> 0.6179775280898876
12 -> 0.6180555555555556
13 -> 0.6180257510729613
14 -> 0.6180371352785146
15 -> 0.6180327868852459
16 -> 0.6180344478216819
17 -> 0.6180338134001252
18 -> 0.6180340557275542
19 -> 0.6180339631667064
20 -> 0.6180339985218034
21 -> 0.6180339850173578

計算機プログラムの構造と解釈

posted with amazlet at 08.11.07

ジェラルド・ジェイ サスマン ジュリー サスマン ハロルド エイブルソン
ピアソンエデュケーション
売り上げランキング: 6542

Amazon.co.jp で詳細を見る