Serendip

Web Studio

問題2.92

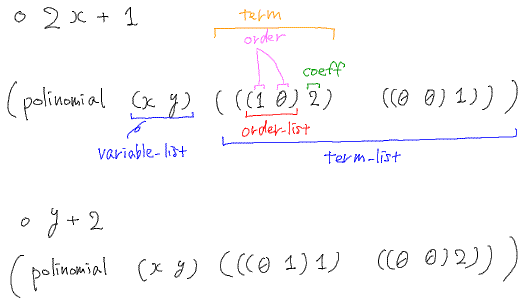
多項式のデータオブジェクトを変数リスト（variable-list）と項リスト（term-list）によって構成する。
項リスト（term-list）は項（term）から成るリストで、各項（term）は次数リスト（order-list）と係数（coeff）によって構成される。
次数リスト（order-list）は変数リスト（variable-list）の順番で各変数の次数（order）が格納される。

異なる変数の多項式の算術演算パッケージ。

(define (install-polynomial-package)
  ;; 内部手続き
  (define (make-poly variable-list term-list)
    (cons variable-list term-list))
  (define (variable-list p) (car p))
  (define (term-list p) (cdr p))
  (define (order-list term) (car term))
  (define (same-order? order-list1 order-list2)
    (equal? order-list1 order-list2))
  (define (=zero-term? L)
    (or (empty-termlist? L)
        (and (=zero? (coeff (first-term L)))
             (=zero-term? (rest-terms L)))))
  (define (=polynomial-zero? p)
    (=zero-term? (term-list p)))
  (define (adjoin-term term term-list)
    (if (=zero? (coeff term))
        term-list
        (cons term term-list)))
  (define (the-empty-termlist) '())
  (define (first-term term-list) (car term-list))
  (define (rest-terms term-list) (cdr term-list))
  (define (empty-termlist? term-list) (null? term-list))
  (define (make-term order-list coeff) (list order-list coeff))
  (define (coeff term) (cadr term))

  ;; order-list1 が高ければ 1 、逆は 2 、同じは 0 を返す.
  (define (order-level order-list1 order-list2)
    (if (null? order-list1)
        0
        (let ((o1 (car order-list1)) (o2 (car order-list2)))
             (cond ((> o1 o2) 1)
                   ((< o1 o2) 2)
                   (else
                     (order-level (cdr order-list1) (cdr order-list2)))))))

  (define (add-terms L1 L2)
    (cond ((empty-termlist? L1) L2)
          ((empty-termlist? L2) L1)
          (else
            (let ((t1 (first-term L1)) (t2 (first-term L2)))
                 (let ((ol (order-level (order-list t1) (order-list t2))))
                      (cond ((= ol 1)
                             (adjoin-term
                               t1 (add-terms (rest-terms L1) L2)))
                            ((= ol 2)
                             (adjoin-term
                               t2 (add-terms L1 (rest-terms L2))))
                            (else
                              (adjoin-term
                                (make-term (order-list t1)
                                           (add (coeff t1) (coeff t2)))
                                (add-terms (rest-terms L1)
                                           (rest-terms L2))))))))))

  (define (mul-terms L1 L2)
    (if (empty-termlist? L1)
        (the-empty-termlist)
        (add-terms (mul-term-by-all-terms (first-term L1) L2)
                   (mul-terms (rest-terms L1) L2))))

  (define (mul-term-by-all-terms t1 L)
    (if (empty-termlist? L)
        (the-empty-termlist)
        (let ((t2 (first-term L)))
             (adjoin-term
               (make-term (mul-order-list (order-list t1) (order-list t2))
                          (mul (coeff t1) (coeff t2)))
               (mul-term-by-all-terms t1 (rest-terms L))))))

  (define (mul-order-list order-list1 order-list2)
    (if (null? order-list1)
        '()
        (cons (add (car order-list1)
                   (car order-list2))
              (mul-order-list (cdr order-list1)
                              (cdr order-list2)))))

  (define (add-poly p1 p2)
    (make-poly (order-list p1)
               (add-terms (term-list p1)
                          (term-list p2))))

  (define (mul-poly p1 p2)
    (make-poly (order-list p1)
               (mul-terms (term-list p1)
                          (term-list p2))))

  (define (sub-poly p1 p2)
    (make-poly (order-list p1)
               (add-terms (term-list p1)
                          (negative-term (term-list p2)))))

  (define (negative-poly p)
    (make-poly (order-list p) (negative-term (term-list p))))

  (define (negative-term L)
    (if (empty-termlist? L)
        (the-empty-termlist)
        (let ((t (first-term L)))
             (adjoin-term
               (make-term (order-list t) (negative (coeff t)))
               (negative-term (rest-terms L))))))

  ;; システムの他の部分とのインターフェース
  (define (tag p) (attach-tag 'polynomial p))
  (put 'add '(polynomial polynomial)
       (lambda (p1 p2) (tag (add-poly p1 p2))))
  (put 'mul '(polynomial polynomial)
       (lambda (p1 p2) (tag (mul-poly p1 p2))))
  (put 'negative '(polynomial)
       (lambda (p) (tag (negative-poly p))))
  (put 'sub '(polynomial polynomial)
       (lambda (p1 p2) (tag (sub-poly p1 p2))))
  (put '=zero? '(polynomial) =polynomial-zero?)
  (put 'make 'polynomial
       (lambda (var terms) (tag (make-poly var terms))))
  (put 'debug '(polynomial) term-list)
  'done)

(define (make-polynomial var terms)
  ((get 'make 'polynomial) var terms))

(install-polynomial-package)

実行結果

(define p1 (make-polynomial '(x y) '(((1 0) 2) ((0 0) 1)))) ;; => 2x + 1
;(polynomial (x y) ((1 0) 2) ((0 0) 1))
(define p2 (make-polynomial '(x y) '(((0 1) 1) ((0 0) 2)))) ;; y + 2
;(polynomial (x y) ((0 1) 1) ((0 0) 2))
(define p3 (make-polynomial '(x y) '(((2 0) 4) ((1 0) 1) ((0 0) 3)))) ;; => 4x^2 + x + 3
;(polynomial (x y) ((2 0) 4) ((1 0) 1) ((0 0) 3))
(define p4 (make-polynomial '(x y) '(((1 0) 2) ((0 0) 3) ((1 2) 1)))) ;; => 2x + 3 + xy^2
;(polynomial (x y) ((1 0) 2) ((0 0) 3) ((1 2) 1))

(add p1 p2) ;; => 2x + y + 3
gosh> (polynomial (x y) ((1 0) 2) ((0 1) 1) ((0 0) 3))
(sub p1 p2) ;; => 2x - y -1
gosh> (polynomial (x y) ((1 0) 2) ((0 1) -1) ((0 0) -1))
(mul p1 p2) ;; => 2xy + 4x + y + 2
gosh> (polynomial (x y) ((1 1) 2) ((1 0) 4) ((0 1) 1) ((0 0) 2))
(add p3 p4) ;; => 4x^2 + 3x + 6 + xy^2
gosh> (polynomial (x y) ((2 0) 4) ((1 0) 3) ((0 0) 6) ((1 2) 1))
(sub p3 p4) ;; => 4x^2 - x - xy^2
gosh> (polynomial (x y) ((2 0) 4) ((1 0) -1) ((1 2) -1))
(mul p3 p4) ;; => 8x^3 + 12x^2 + 4x^3y^2 + 2x^2 + 3x + x^2y^2 + 6x + 9 + 3xy^2 => 8x^3 + 14x^2 + 4x^3y^2 + 9x + x^2y^2 + 9 + 3xy^2
gosh> (polynomial (x y) ((3 0) 8) ((2 0) 14) ((3 2) 4) ((1 0) 9) ((2 2) 1) ((0 0) 9) ((1 2) 3))

計算機プログラムの構造と解釈

posted with amazlet at 08.11.07

ジェラルド・ジェイ サスマン ジュリー サスマン ハロルド エイブルソン
ピアソンエデュケーション
売り上げランキング: 6542

Amazon.co.jp で詳細を見る